Для самых маленьких: Шифрование

На всякий случай уделим немного времени терминологии, чтобы далее по тексту не возникало путаницы.

Кодирование - это представление информации в виде, пригодном для фиксации, передачи и/или обработки с возможностью последующего восстановления. Примером кодирования может служить преобразование текста в набор тире, точек и пауз при помощи азбуки Морзе. Или представление текстовой информации в виде чисел для помещения в память компьютера(к этому еще вернемся).

Шифрование - это такое изменение информации, которое позволяет восстановить ее исходное состояние только авторизованному кругу лиц, обладающих некоторым секретом и, напротив, делает эту задачу крайне сложной для неавторизованных лиц, этим секретом не располагающим.

Несмотря на то, что некоторые способы кодирования крайне сложны для восприятия лицами, не располагающими некоторыми знаниями или оборудованием (например, все та же азбука Морзе, шрифт Брайля или же электромагнитные колебания в радиосвязи), задачи кодирования и шифрования сильно отличаются и, более того, в узком понимании являются противоположными, но не взаимоисключающими.

Таким образом, поскольку рассматриваемые далее алгоритмы шифрования оперируют числами, информацию необходимо привести к виду, пригодному для обработки, т. е. по определению закодировать. Для примеров я буду использовать слово SECRET. Закодируем его при помощи таблицы символов ASCII.

Так исходное слово SECRET превращается в следующий набор чисел: 83 69 67 82 69 84. Поскольку я говорил, что пост предназначен для неопределенного круга лиц, поясню, что в колонке Char находится кодируемый символ, а в колонке Dec соответствующее ему десятичное число. Первые 32 символа не пустые - они просто являются непечатаемыми (символ переноса строки, символ возврата каретки и т. д.), поэтому если с ними придется столкнуться, я заменю их символом подчеркивания (_).

Я думаю, цели кодирования и шифрования мы уяснили, поэтому двинемся дальше.

Симметричным называется такой вид шифрования, в котором шифрование и дешифрование производятся одним и тем же ключом. Пожалуй, одним из самых простых и доступных видов симметричного шифрования является сдвиговый шифр Цезаря. Суть его очень проста - давайте увеличим каждое из чисел, полученных в результате кодирования слова SECRET на любое произвольное число, которое будет выступать в роли ключа.

\begin{equation} C_n = M_n + k\\ M_n = C_n - k \end{equation}

Не пугайтесь, формулы по тексту будут, но для их понимания достаточно уровня начальной школы. Итак, M - это число(код символа) в исходном сообщении. Наше сообщение состоит из 6 символов, поэтому эту операцию придется выполнить 6 раз. С - это шифротекст, т. е. новое число, по задумке лишенное смысла для человека, не обладающего ключом. Ну и k - это наш ключ, которым должны обладать обе стороны - шифрующая и дешифрующая. n это, как несложно догадаться, положение символа в исходной и результирующей строке.

Давайте возьмем для простоты число 1 в качестве ключа и выполним шифрование. Наше исходное сообщение M 83 69 67 82 69 84 превращается в шифротекст C 84 70 68 83 70 85. Думаю, я более чем подробно объяснил суть пребразования. Теперь давайте выполним декодирование при помощи все той же таблицы символов ASCII и из исходного SECRET получим TFDSFU, можете перепроверить. Чтож, желаемого результата мы достигли - невооруженным глазом усмотреть смысл в шифротексте сможет не каждый. Тем не менее, таким образом вы сможете скрыть сообщение, разве что, от своего домашнего питомца - на ручной подбор ключа уйдет пара минут, а компьютер справится за настолько малое время, что им можно пренебречь и сказать "моментально". Но, по всей видимости, почти 2100 лет назад этого было вполне достаточно.

К слову, если верить Википедии, шифром цезаря можно называть сдвиговый шифр, в котором в качестве ключа используется число 3. А наш шифр с ключом 1, можно вольно назвать шифром Августа - племянника Цезаря.

Думаю, процесс дешифрования можно опустить в силу его простоты, если не сказать интуитивности. Добавлю только, что в качестве ключа можно использовать не одно число, а набор чисел, равный или превосходящий по количеству размер шифруемого сообщения.

\begin{equation} C_n = M_n + K_n \\ M_n = C_n - K_n \end{equation}

Так, например, в качестве ключа можно использовать слово ENIGMA, равное по размеру шифруемому сообщению, предварительно закодировав его. Получим 69 78 73 71 77 65. Теперь, просуммировав соответствующие числа из сообщения и ключа, получим 83+69 69+78 67+73 82+71 69+77 84+65 или 152 147 140 153 146 149. Декодировать числа, превосходящие 127 (размер таблицы символов), не получится, поэтому придется либо воспользоваться операцией x mod y, что означает остаток от деления x на y (где x - код символа в шифротексте, а y - размер алфавита, т. е. 127), либо не выполнять декодирование шифротекста и передавать его в виде чисел.

Такой вариант сдвигового шифрования является значительно более стойким по сравнению с первым, поскольку один и тот же символ в исходном тексте может соответстовать разным символам в шифротексте и наоборот. На всякий случай, размещу итоговый вариант сдвигового шифра.

\begin{equation} C_n = (M_n + K_n) \bmod l \\ M_n = (C_n - K_n + l) \bmod l \end{equation}

Где l - размер алфавита. Нужно ли прибавлять l при дешифровке зависит от реализации вычисления остатка от деления, но в целом - лишним не будет.

Ну и в заключение рассказа о простых симметричных шифрах скажу пару слов о шифре на основе операции xor (если читатель не знаком с битовыми операциями - можно переходить к асимметричным шифрам), не менее известном, чем сдвиговые шифры. Прелесть операции xor в том, что для нее верно следующее:

\begin{equation} a \oplus a = 0 \\ a \oplus 0 = a \\ a \oplus b \oplus c = (a \oplus b) \oplus c = a \oplus (b \oplus c) \end{equation}

Следовательно легко доказать, что

\begin{equation} C_n = M_n \oplus k \\ M_n = C_n \oplus k \end{equation}

Чтож, думаю это было достаточно подробно и тему симметричного шифрования в рамках данного поста можно закрывать.

Асимметричным называется такой вид шифрования, в котором шифрование и дешифрование производятся различными ключами.

Я не силен в графике, но смысл примерно следующий:

При этом шифротекст не может быть дешифрован в исходный текст при помощи ключа, которым он был зашифрован. Это очень удобно, поскольку избавляет от необходимости согласования общего ключа и, как минимум, вдвое сокращает вероятность скомпрометировать секретный ключ, поскольку он теперь находится только у одного человека - адресата сообщения. Публичный же ключ можно без опасений публиковать где угодно, поскольку он годится только для зашифрования.

Одним из наиболее распространенных алгоритмов асимметричного шифрования на сегодняшний день является RSA. Я не буду сразу говорить о самом алгоритме шифрования-дешифрования т. к. для начала нам понадобится ключ, который чуть сложнее, чем в алгоритмах, описанных выше.

Для начала нам понадобятся два произвольных простых числа - p и q. Напомню, на всякий случай, что простыми числами называются числа, не имеющие делителей кроме себя и единицы (ну мало ли, кто забыл или еще не знает). Примем за p число 11, а за q число 13. Я выбрал эти числа потому что их произведение немногим более нашего размера алфавита, и в то же время не слишком велико, чтобы можно было пользоваться калькулятором. На практике столь малые числа не используются. Совсем. Но для демонстрации алгоритма - сойдет. Теперь нам нужно вычислить числа n и m, и подобрать число e следующим образом:

\begin{equation} n = p * q \\ m = \varphi(n) = (p - 1) * (q - 1) \\ 1 < e < m \end{equation}

При этом e должно быть взаимно простым (т. е. не иметь общих делителей) с числом m. В качестве e нам подойдет число 7. Ну и последнее, что осталось сделать для генерации ключей, это найти такое число d, для которого верно следующее:

\begin{equation} e * d \bmod m = 1 \end{equation}

Нам подойдет число d равное 103.

На этом генерация ключей завершена. Числа e и n формируют публичный ключ, а числа d и n - приватный.

Допустим, я опубликовал числа e и n, равные 7 и 143 соответственно, и кто-то решил отправить мне секретное сообщение.

Процесс шифрования будет выглядеть следующим образом:

\begin{equation} C_i = M_i^e \bmod n \end{equation}

Чтобы зашифровать слово SECRET, закодированное в ASCII (83 69 67 82 69 84), нам снова придется проделать операцию шифрования 6 раз. Для наглядности я распишу процесс шифрования каждого символа.

\begin{equation} C_0 = 83^7 \bmod 143 = 8 \\ C_1 = 69^7 \bmod 143 = 108 \\ C_2 = 67^7 \bmod 143 = 89 \\ C_3 = 82^7 \bmod 143 = 69 \\ C_4 = 69^7 \bmod 143 = 108 \\ C_5 = 84^7 \bmod 143 = 72 \end{equation}

Получили зашифрованное сообщение 8 108 89 69 108 72 или _lYElH. Восстановить исходное сообщение, зная числа 7 и 143, которыми оно было зашифровано, уже не получится (вообще-то, получится потому что они очень малы, но, как я уже говорил - на практике используются числа на десятки порядков превосходящие те, что применяли мы).

Небольшое отступление: с возведением в 7 степень трехзначного числа справится не каждый калькулятор, а ниже по тексту нужно будет возводить в трехзначную степень и "в лоб" это уже тожно ни один калькулятор не сделает. Но можно воспользоваться следующим свойством остатка от деления:

\begin{equation} x^y \bmod n = (x \bmod n) * (x^{y-1} \bmod n) \end{equation}

Собственно, при программировании микроконтроллеров этим приходится пользоваться потому как результируюее число после возведения в степень попросту не поместится в оперативную память (даже при наших малых числах, а в реальном применении - и подавно), поэтому все сводится к циклу нахождения остатка от деления и умножения. Тем не менее, gnome-calculator и большинство программных калькуляторов выполнят все оптимизации самостоятельно - главное описать им задачу целиком, а не пытаться решить ее по действиям.

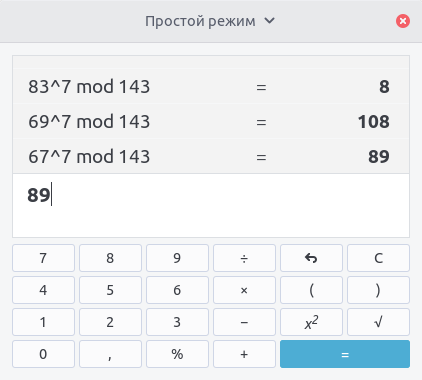
Ну, дело за малым - осталось расшифровать полученное сообщение 8 108 89 69 108 72. Для этого нам понадобится секретный ключ, состоящий из чисел d и n, равных 103 и 143 соответственно. Дешифрование очень похоже на зашифрование за исключением, разве что, показателя степени:

\begin{equation} M_i = C_i^d \bmod n \end{equation}

Пробуем вычислить

\begin{equation} C_0 = 8^{103} \bmod 143 = 83 \\ C_1 = 108^{103} \bmod 143 = 69 \\ C_2 = 89^{103} \bmod 143 = 67 \\ C_3 = 69^{103} \bmod 143 = 82 \\ C_4 = 108^{103} \bmod 143 = 69 \\ C_5 = 72^{103} \bmod 143 = 84 \end{equation}

Вуаля! Мы получили исходное сообщение 83 69 67 82 69 84 или SECRET. Поздравляю, на этом изложение сути асимметричного шифрования в рамках данного поста можно считать завершенным.

Использовать в жизни то, что здесь описано в незменном виде ни в коем случае нельзя. Так, например, способ, которым был продемонстрирован алгоритм RSA, по сути, остается обыкновенным шифром подстановки, поскольку каждому исходному символу соответствует только один результирующий. Если бы мы использовали значительно большие числа, чем эти - мы могли бы шифровать по нескольку (4, 8) символов сразу, плюс добавлять к исходному тексту мусор, который бы сводил возможность частотного анализа на нет, или же использовать более продвинутые способы, но этот пост не об этом - он о принципах и лежащих в их основе алгоритмах, которые, я надеюсь, читатель смог уяснить в процессе чтения.

Если же вам нужно шифрование - всегда, когда есть такая возможность, используйте общепринятые утилиты и библиотеки - GnuPG, OpenSSL и иже с ними. В них вложено человекочасов более, чем есть в вашем распоряжении - не тратье их понапрасну (если, конечно, речь не об обучении).